Several flowers are shown at my twitter, Sekinan Library.
SRFL News
Monday, 30 May 2016
Fresh snow, climbing rose
May is the rose season in Japan. We went Jindai botanical garden, Chofu, Tokyo, where Fresh rose blooms fine among the crowded people, The photo is from my garden hedge.
From the garden, white rose, Fresh snow.
Fresh snow is the climbing rose, so popular in Japan. I planted it at the hedge 20 years ago. Still blooms in fine white around the house.
Several flowers are shown at my twitter, Sekinan Library.
Saturday, 28 May 2016
Meaning minimum
Meaning minimum
Meaning minimum
On Roman Jakobson, Sergej Karcevskij and CHINO Eiichi
TANAKA Akio
ifbetrue
6 April 2013
1.
Meaning minimum is one of the kernel concepts for the model of language universals on my study. The concept was at first thought from Roman Jakobson’s semantic minimum on which I first read at his book, ESSAIS DE LINGUISTIGUE GENERALE, 1973. His concept was yet intuitive at the linguistic study history in the latter half of the 20th century.Comparison with his concept, my definition of meaning minimum was a certain basis prepared in the learning of mathematics, especially on algebraic geometry, that is the most fantastic approach to the construction of the language model. But the contents of meaning minimum is vacant. This concept shows the minimum unit of one big constructive meaning of word. meaning minimum seems to be correspondent with element of set theory, which theory and foundations of mathematics had been my favourite mathematical basis in 1970s, my youth time. Bourbaki was always echoed around us. Grothendieck was a highest star in this world.
2.
Time went vast from at that time. Set theory became one of the premise field of mathematics. But in my part, set theory’s agenda was put at a another point. Because language has a certain expanded world that seems to be continuous. Set theory’s atomic discreteness does not match in my primary learning level. So, in my age 30s, I had sank in the philosophically intuitive thinking often referring the tradition of 1920s, especially of the Linguistic Circle of Prague. On the circle my teacher CHINO Eiichi had taught me from time to time on the campus of university or coffee shop near the station we used. CHINO had gone to the Czechoslovakia Republic from 1959 to 1967. I first met him in 1969 at his Russian class at my third year of university student. I was the age 21 and he was 37.
3.
At the age 23’s 1971 spring, I graduated university and once became a high school’s teacher and again returned back to university in 1979 after 8 year job of the school. At that time I thought of characters’ distinctive features on Written Chinese classics. I mainly read WANG Guowei, ZHANG Binglin, DUAN Yucai, WANG yinzhi guiding by Japanese modern scholoar KANO Naoki. Expressly I had attracted to WANG guowei and his book Guantangjilin. Besides reading these China’s Qing dynasty’s linguistic peaks, I had always thought on Ludwig Wittgenstein for his endless pursuit on language. So I resigned school and came back to the campus where I again met with CHINO. I was age 30s and he was 50s. He was already the big scholar at the linguistic field but I was a poor return student. But I dare to say we were colleagues for language study. He taught me the detailed and strict tradition of the linguistic Circle of Prague. He frequently talked on Sergej Karcevskij and his eminent discernment on language. In the later year’s masterpiece, Janua Linguisticae Reserata, 1994, he wrote only Karcevskij as genius in the great linguists.
4.
Being led by CHINO, I again started linguistic learning on meaning that I had been interested in from my 20s but too hard to approach by my talent. This time I had Karcevskij’s fine insight to meaning enough absorbing the fertile tradition of Prague, where also exist Jakobson and Mathesius. Through the learning I gradually lean to desire to write clear definitions on language. I again remembered the little learning of my 20s age’s mathematics. Bourbaki, Godel, TAKEUCHI and their set theory, foundations of mathematics and that Incompleteness theorem. I had learnt mathematics little by little, inch by inch.
5.
CHINO Died in 2002 at age 70 and I became 55. The next year 2003, I wrote a short paper titled “Quantum Theory for Language”. This paper was showed at a international symposium on Silk road for dealing with language from Chinese characters on linguistic viewpoint. I knew that Asian civilisation and history had great concern not only from Asia but also European continents. At the symposium some 400 researchers gathered in the various scholarly fields. It was a awesome encounter for my study, namely, East meet West. Probably Chinese character’s agenda will be written by Europe oriented mathematics. WANG Guowei will meet with karcevskij mediated through mathematics’ description. The target confronted at that time was time inherent in characters, or time in word. In Chinese, particularly in classical written Chinese, all the characters show enough independent meaning in one character probably including even time. It was my first conjecture taught from Karcevskij and CHINO. Meaning minimum is on the boat going across to the opposite shore. This metaphor was derived from WANG Guowei’s famous paper, “Yin- bu zhong suojian xiangong xianwang kao”
6.
The concept of time inevitably led to the distance of distance. In 2004, I wrote a paper titled “Distance Theory”. But the paper was yet intuitive and not clear for descriptive definition. So hereinafter I learnt algebra inch by inch being assisted with the rich heritage of geometry. In the centre of learning, always exist time that connotes finiteness and infinity. But infinity is not easily obtained without probably only loop space at the present. And again returns back to meaning minimum as the passenger of the boat named time property inherent. This time the passenger on the boat is called operad or algebraic language.
7.
After all I came back to the very dream that I had embraced since the high school days. It was a fundamental ask on language related with mathematics and physics. The root of language would be able to describe by mathematics and physics. In my mind language is always put at the centre of the pursuit that was what anyone can clearly understand. Description by mathematics, but physics why (Note 1)?. Physics treats with substance that constructs the world in which I had desire to let language enter. Substantial language(Note 2). It was my dream and will be hereafter (Note 3).
References
1.
<Meaning minimum>
Cell Theory Continuation of Quantum Theory for Language / From Cell to Manifold For LEIBNIZ and JAKOBSON / Tokyo June 2, 2007
<Bourbaki>
The Time of Language Ode to The Early Bourbaki To Grothendieck / January 10, 2012
2.
<CHINO Eiichi>
Fortuitous Meeting What CHINO Eiichi Taught Me in the CLass of Linguistics / Tokyo December 5, 2004
<The Linguistic Circle of Prague>
Linguistic Circle of Prague / Tokyo 13 July 2012, 19 July 2012 Added
3.
<WANG Guowei>
The Complete Works of WANG Guowei / Tokyo 24 May 2012
<Ludwig Wittgenstein>
The Time of Wittgenstein / Tokyo January 20, 2012
<Sergej Karcevskij>
Notes for KARCEVSKIJ Sergej / Note for KARCEVSKIJ Sergej’s “Du dualisme asymetrique du signe linguistique” / Tokyo September 8, 2011
4.
<Set Theory>
Quantum Linguistics / Growth of Word Dedicated to TAKEUCHI Gaishi / Tokyo January 30, 2006
5.
<Quantum Theory for Language>
Quantum Theory for Language Synopsis / Tokyo January 15, 2004
<Time inherent in characters>
On Time Property Inherent in Characters / Hakuba March 28, 2003
6.
<Distance>
Distance Theory / Tokyo May 5, 2004
<Meaning minimum and distance>
sekinanlogos / Floer Homology Language / Supersymmetric Harmonic Oscillator / Tokyo May 6, 2009
<Loop space>
sekinanmodel / Infinite Loop Space Language / Word as Infinite Loop Space / 6 December 2012
<Operad>
ifbetruezoho / Operad Meaning Theory / From Cell to Operad / 4 March 2013
7.
<Description>
sekinanmetria / Notes for KARCEVSKIJ Sergej / Description of Language / September 9, 2011
<Substantiality>
sekinanlogos / Floer Homology Language / Potential of Language / Tokyo June 16, 2009
<Amalgamation>
Language, amalgamation of mathematics and physics / ifbetrue 2 April 2013
# Here ends the paper.
[Additional notes, 14 September 2014]
1. Roger Penrose / 25 October 2012
2. Substantiality Dedicated to SAPIR Edward / 27 February 2005
3. Perhaps Return to Physics / 16 August 2014
On Roman Jakobson, Sergej Karcevskij and CHINO Eiichi
TANAKA Akio
ifbetrue
6 April 2013
1.
Meaning minimum is one of the kernel concepts for the model of language universals on my study. The concept was at first thought from Roman Jakobson’s semantic minimum on which I first read at his book, ESSAIS DE LINGUISTIGUE GENERALE, 1973. His concept was yet intuitive at the linguistic study history in the latter half of the 20th century.Comparison with his concept, my definition of meaning minimum was a certain basis prepared in the learning of mathematics, especially on algebraic geometry, that is the most fantastic approach to the construction of the language model. But the contents of meaning minimum is vacant. This concept shows the minimum unit of one big constructive meaning of word. meaning minimum seems to be correspondent with element of set theory, which theory and foundations of mathematics had been my favourite mathematical basis in 1970s, my youth time. Bourbaki was always echoed around us. Grothendieck was a highest star in this world.
2.
Time went vast from at that time. Set theory became one of the premise field of mathematics. But in my part, set theory’s agenda was put at a another point. Because language has a certain expanded world that seems to be continuous. Set theory’s atomic discreteness does not match in my primary learning level. So, in my age 30s, I had sank in the philosophically intuitive thinking often referring the tradition of 1920s, especially of the Linguistic Circle of Prague. On the circle my teacher CHINO Eiichi had taught me from time to time on the campus of university or coffee shop near the station we used. CHINO had gone to the Czechoslovakia Republic from 1959 to 1967. I first met him in 1969 at his Russian class at my third year of university student. I was the age 21 and he was 37.
3.
At the age 23’s 1971 spring, I graduated university and once became a high school’s teacher and again returned back to university in 1979 after 8 year job of the school. At that time I thought of characters’ distinctive features on Written Chinese classics. I mainly read WANG Guowei, ZHANG Binglin, DUAN Yucai, WANG yinzhi guiding by Japanese modern scholoar KANO Naoki. Expressly I had attracted to WANG guowei and his book Guantangjilin. Besides reading these China’s Qing dynasty’s linguistic peaks, I had always thought on Ludwig Wittgenstein for his endless pursuit on language. So I resigned school and came back to the campus where I again met with CHINO. I was age 30s and he was 50s. He was already the big scholar at the linguistic field but I was a poor return student. But I dare to say we were colleagues for language study. He taught me the detailed and strict tradition of the linguistic Circle of Prague. He frequently talked on Sergej Karcevskij and his eminent discernment on language. In the later year’s masterpiece, Janua Linguisticae Reserata, 1994, he wrote only Karcevskij as genius in the great linguists.
4.
Being led by CHINO, I again started linguistic learning on meaning that I had been interested in from my 20s but too hard to approach by my talent. This time I had Karcevskij’s fine insight to meaning enough absorbing the fertile tradition of Prague, where also exist Jakobson and Mathesius. Through the learning I gradually lean to desire to write clear definitions on language. I again remembered the little learning of my 20s age’s mathematics. Bourbaki, Godel, TAKEUCHI and their set theory, foundations of mathematics and that Incompleteness theorem. I had learnt mathematics little by little, inch by inch.
5.
CHINO Died in 2002 at age 70 and I became 55. The next year 2003, I wrote a short paper titled “Quantum Theory for Language”. This paper was showed at a international symposium on Silk road for dealing with language from Chinese characters on linguistic viewpoint. I knew that Asian civilisation and history had great concern not only from Asia but also European continents. At the symposium some 400 researchers gathered in the various scholarly fields. It was a awesome encounter for my study, namely, East meet West. Probably Chinese character’s agenda will be written by Europe oriented mathematics. WANG Guowei will meet with karcevskij mediated through mathematics’ description. The target confronted at that time was time inherent in characters, or time in word. In Chinese, particularly in classical written Chinese, all the characters show enough independent meaning in one character probably including even time. It was my first conjecture taught from Karcevskij and CHINO. Meaning minimum is on the boat going across to the opposite shore. This metaphor was derived from WANG Guowei’s famous paper, “Yin- bu zhong suojian xiangong xianwang kao”
6.
The concept of time inevitably led to the distance of distance. In 2004, I wrote a paper titled “Distance Theory”. But the paper was yet intuitive and not clear for descriptive definition. So hereinafter I learnt algebra inch by inch being assisted with the rich heritage of geometry. In the centre of learning, always exist time that connotes finiteness and infinity. But infinity is not easily obtained without probably only loop space at the present. And again returns back to meaning minimum as the passenger of the boat named time property inherent. This time the passenger on the boat is called operad or algebraic language.
7.
After all I came back to the very dream that I had embraced since the high school days. It was a fundamental ask on language related with mathematics and physics. The root of language would be able to describe by mathematics and physics. In my mind language is always put at the centre of the pursuit that was what anyone can clearly understand. Description by mathematics, but physics why (Note 1)?. Physics treats with substance that constructs the world in which I had desire to let language enter. Substantial language(Note 2). It was my dream and will be hereafter (Note 3).
References
1.
<Meaning minimum>
Cell Theory Continuation of Quantum Theory for Language / From Cell to Manifold For LEIBNIZ and JAKOBSON / Tokyo June 2, 2007
<Bourbaki>
The Time of Language Ode to The Early Bourbaki To Grothendieck / January 10, 2012
2.
<CHINO Eiichi>
Fortuitous Meeting What CHINO Eiichi Taught Me in the CLass of Linguistics / Tokyo December 5, 2004
<The Linguistic Circle of Prague>
Linguistic Circle of Prague / Tokyo 13 July 2012, 19 July 2012 Added
3.
<WANG Guowei>
The Complete Works of WANG Guowei / Tokyo 24 May 2012
<Ludwig Wittgenstein>
The Time of Wittgenstein / Tokyo January 20, 2012
<Sergej Karcevskij>
Notes for KARCEVSKIJ Sergej / Note for KARCEVSKIJ Sergej’s “Du dualisme asymetrique du signe linguistique” / Tokyo September 8, 2011
4.
<Set Theory>
Quantum Linguistics / Growth of Word Dedicated to TAKEUCHI Gaishi / Tokyo January 30, 2006
5.
<Quantum Theory for Language>
Quantum Theory for Language Synopsis / Tokyo January 15, 2004
<Time inherent in characters>
On Time Property Inherent in Characters / Hakuba March 28, 2003
6.
<Distance>
Distance Theory / Tokyo May 5, 2004
<Meaning minimum and distance>
sekinanlogos / Floer Homology Language / Supersymmetric Harmonic Oscillator / Tokyo May 6, 2009
<Loop space>
sekinanmodel / Infinite Loop Space Language / Word as Infinite Loop Space / 6 December 2012
<Operad>
ifbetruezoho / Operad Meaning Theory / From Cell to Operad / 4 March 2013
7.
<Description>
sekinanmetria / Notes for KARCEVSKIJ Sergej / Description of Language / September 9, 2011
<Substantiality>
sekinanlogos / Floer Homology Language / Potential of Language / Tokyo June 16, 2009
<Amalgamation>
Language, amalgamation of mathematics and physics / ifbetrue 2 April 2013
# Here ends the paper.
[Additional notes, 14 September 2014]
1. Roger Penrose / 25 October 2012
2. Substantiality Dedicated to SAPIR Edward / 27 February 2005
3. Perhaps Return to Physics / 16 August 2014
Wednesday, 25 May 2016
Derived Category Language, 25 May 2016 Edition
Derived Category Language, 25 May 2016 Edition
- Bridge between mathematics and physics / revised
- Kontsevich's conjecture Category theoretic mirror symmetry conjecture
- Derived Category Language 1
- Karcevskij conjecture 1928 and Kawamata conjecture 2002
- Additional meaning and embedding
- Derived Category Language 2
- Language stability and triangulated category
- Derived Category Language 3
Read more: http://srfl-theory.webnode.com/news/derived-category-language/
Derived Category Language 3
Derived Category Language 3
Language stability and triangulated category
[Epitome]
Language's stability presented by Sergej Karcevskij in 1928.
tability conditions on triangulated categoriesData ( Z, A ) satisfies the next condition.
is bounded kernel of t-structure.
gives stability condition on A .
------------------------------------------------------------------------------------------------------
2.
[Paper on Karcevskij conjecture by TANAKA Akio 2011]
Condition of Meaning
TANAKA Akio
September 11, 2011
TANAKA Akio
September 11, 2011
[Preparation]
Graded differential algebra 
Minimal model of graded differential algebra 
Degree of homogenious element x of graded differential algabra |x|
Basis of linear space is given by homogenious and elements x1, ....., xn
N (V) = L (V) k = N ( x 1 , ....., x n )
Operation of minimal model 
Spherical surface Sn, n≥2
de Rham complex 
*(Sn)
*(Sn)
When n iseaven number,
Volume element of Sn 
Mn = Λ (x), |x| = n, dx = 0,
, 
M2n-1 gives minimal model Sn to de Rham complex 
.
.
When n is odd number,
Mn gives minimal model Sn to de Rham complex .
.
[Interpretation]
Word is given by spherical surface.
Meaning of word is given by elements x1, ....., xn.
Word has minimal model.
Word becomes formal.
Fundamental group of word contains free group of rank b1(M).
Here KARCEVSKIJ's "stable part" is identified to fundamental group and " mobile part" is identified to free group.
--------------------------------------------------------------------------------------------
3.
[Paper on description of language by TANAKA Akio 2011]
[Paper on description of language by TANAKA Akio 2011]
Description of Language
TANAKA Akio
September 9, 2011
TANAKA Akio
September 9, 2011
Manifold M
Cup product map of M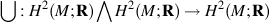 
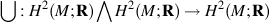
Dual map of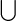 
Free Lie algebra that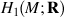 
generates £ ( 
)
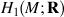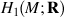generates £ ( )
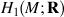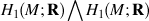is identified as the partial space of £( 
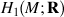) that quadrastic Lie bracket of 
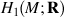generates.
Ideal of £(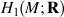 
) that Im η generates a
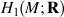) that Im η generates a
Holonomy Lie algebra of M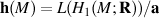 
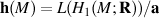
Completion of holonomy Lie algebra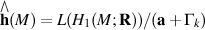 
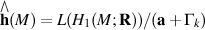
If M has quadrastic homology connection, Malcev completion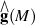 
becomes isomorphic with holonoly Lie algebra completion 
.
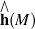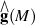becomes isomorphic with holonoly Lie algebra completion .
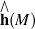Primary minimum model M(1)of differential manifold M is isomorphic with Malcev completion of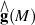 
of M's fundamental group.
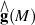of M's fundamental group.
For the description of a language model there is a need primary minimum model M(1) of differential manifold M.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
All rights reserved.
© 2011 by The Sekinan Research Field of Language
-----------------------------------------------------------------------------------------------------------
4.
[Note]
If word satisfies Bridgeland 2002's Data{Z, A] , word has a stability in language.
For the problem of additional meaning refer to Karcevskij conjecture 1928 and Kawamata conjecture 2002.
-----------------------------------------------------------------------------------------------------
#This paper is unfinished
Tokyo
25 May 2016
SRFL Theory
25 May 2016
SRFL Theory
Read more: http://srfl-theory.webnode.com/news/derived-category-language-3/
Monday, 23 May 2016
Language stability and triangulated category
T. Bridgeland defined stability conditions on triangulated categories in 2007.
Language's stability presented by Sergej Karcevskij in 1928.
Bridgeland's stability seems to hint for Karcevskij's stability.
This paper is unfinished.
Tokyo
23 May 2016
SRFL Theory
Bridgeland's stability seems to hint for Karcevskij's stability.
This paper is unfinished.
Tokyo
23 May 2016
SRFL Theory
Sekinan Archive - Invitation to language universals
Invitation to Essays and Papers of Sekinan Library
Leading Essay
Coffee shop named California
Meaning Minimum
Invitational Dialogue
Why do you think that language has structure?
Overview of Study
Basis of Study
Sekinan Archive shows the invitational data on language universals to the researchers.
Half farewell to Sergej Karcevskij and the Linguistic Circle of Prague
Road to Language Universals
Tokyo
27 December 2015
Present Work
SRFL Group
Sekinan Group
SIL Group
Blog
Facebook
Google＋
Sekinan Group
SIL Group
Blog
Google＋
Additional meaning and embedding
Additional meaning and embedding
1.Derived category
Category theoretic mirror symmetry conjecture
1.
Fukaya category is
Fuk(X, ω).
Fuk(X, ω).
2.
General symplectic manifold is
.
3.
General symplectic manifold is
.3.
Derived category of A∞
is 
.
is .
4.
Conjecture
Conjecture
When
and 
have physical mirror relation,
there exists the next triangle category's equivalence
2.Embedding
Derived Category Language 2
Kawamata Conjecture
Conjecture
is birational map between smooth objective algebraic manifolds.
And
.
At This condition,
there exists next fully faithful embedding.
3.Stable and mobile
Condition of Meaning
TANAKA Akio
September 11, 2011
TANAKA Akio
September 11, 2011
[Preparation]
Graded differential algebra
Minimal model of graded differential algebra
Degree of homogenious element x of graded differential algabra |x|
Basis of linear space is given by homogenious and elements x1, ....., xn
Λ (V) = Λ(V)k =Λ (x1, ....., xn )
Operation of minimal model
<Example>
Spherical surface Sn, n≥2
de Rham complex *(Sn)
*(Sn)
When n iseaven number,
Volume element of Sn
Mn = Λ (x), |x| = n, dx = 0,
,
M2n-1 gives minimal model Sn to de Rham complex .
.
When n is odd number,
Mn gives minimal model Sn to de Rham complex .
.
[Interpretation]
Word is given by spherical surface.
Meaning of word is given by elements x1, ....., xn.
Word has minimal model.
Word becomes formal.
Fundamental group of word contains free group of rank b1(M).
Here KARCEVSKIJ's "stable part" is identified to fundamental group and " mobile part" is identified to free group.
Refer to the paper Notes for KARCEVSKIJ Sergej, "Dusualisme asymétrique du signe linguistique" .
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
All rights reserved.
© 2011 by The Sekinan Research Field of Language
4.Additional meaning
For the Supposition of KARCEVSKIJ Sergej
Completion of Language
September 23, 2011
[Preparation]
1.
n dimensional complex space Cn
Open set 
Whole holomorphic function over U 
Ring sheaf for
U →Oan(U)
Complex analytic manifold Cann
Algebraic manifold An multinomial of Cann
Ideal of multinomial ring a 
[x1, x2, ..., xn]
[x1, x2, ..., xn]
V(a) = {(a1, a2, ..., an) 
Cn f (a1, a2, ..., an) = 0, 
a }
Cn f (a1, a2, ..., an) = 0, a }
Whole closed set of V(a) 
Fundamental open set D(f) = {(a1, a2, ..., an) Cn | f (a1, a2, ..., an) ≠ 0}
Cn | f (a1, a2, ..., an) ≠ 0}
Arbitrary family of open set {Ui} 
Easy sheaf F 
Zariski topological space
Ring sheaf O
Affine space An = ( , O)
, O)
Ring R
Set of whole maximum ideal Spm R1
Spm R Spectrum of R
<Proposition>
Spm R is Noether- like.
◊
<Proposition>
R is integral domain.
Whole of open sets without null set Ux
Quotient field K
Mapping from Ux to whole partial set of K O
O(V(a)c) = 
Rf
Rf
c expresses complementary set.
O is easy sheaf of ring over Spm R that is whole set K.
◊
<Definition>
R is finite generative integral domain over k.
Triple (i) (ii) (iii) is called affine algebraic variety.
(i) Set Spm R
(ii) Zariski topology
(iii) Ring's sheaf O
O is called structure sheaf of affine algebraic variety.
◊
Ring homomorphism between definite generative integral domains 
Upper is expressed by 
.
.
Ring holomorphism OX(U) → OY((t
)-1U)
)-1U)
Morphism from affine algebraic variety Y to X ( OX(U) → OY((t )-1U), X→Y )
)-1U), X→Y )
When 
is surjection, t is isomorphism overclosed partial set defined by p= Ker 
.
is surjection, t is isomorphism overclosed partial set defined by p= Ker .
Upper is called to closed immersion.
2.
Ring holomorphism
Morphism between affine algebraic varieties 
Kernel of 
p
p
Image of 
<Definition>
It is called that when is injection 
is dominant.
is injection is dominant.
◊
<Definition>
R is medium ring between S and its quotient field K.
When that is given by natural injection is isomorphism over open set, is called open immersion.
that is given by natural injection is isomorphism over open set, is called open immersion.
◊
<Definition>
When X is algebraic variety, longitude of maximum chain is equal to transcendental dimension of function field k(X).
It is called dimension of algebraic variety X, expressed by dim X.
◊
<Definition>
Defined generative field over k K
Space ( X, Ox )added ring that is whole sets of K that has open covers {Ui}
satisfies next conditions is called algebraic variety.
satisfies next conditions is called algebraic variety.
(i) Each Ui is affine algebraic variety that has quotient K .
(ii) For each i, j 
I, intersection 
is open partial set of 
.
I, intersection is open partial set of .
◊
3.
<Definition>
Tensor product between ring and itself becomes ring by each elements products.
Elements 
that defines surjective homomorphism is expressed by 
.
that defines surjective homomorphism is expressed by .
Image 
of closed embedding defined by is called diagonal.
of closed embedding defined by is called diagonal.
◊
<Definition>
Field K
Ringed space that have common whole set K (A, OA) (B, OB)
Topological space C
Open embedding 
A and B have common partial set C.
Topological space glued A and B by C 
Easy sheaf over W OW
ahere, arbitrary open set Ø ≠ 
Ringed space 
is called glue of A and B by C.
is called glue of A and B by C.
◊
<Definition>
Intedgral domains that have common quotient field K R, S
Element R am ≠ 0
Element S bn ≠ 0
Spm T 
Spm R, Spm T 
Spm S
Spm R, Spm T Spm S
Glue defined by the upper is called simple.
◊
<Definition>
Affine algebraic varieties U1, U2
Common open set of U1, U2 UC
Diagonal embedding 
When the upper is closed set, glue is called separated.
◊
<Proposition>
For simple glue 
, next is equivalent.
, next is equivalent.
(*) It is separated.
(**) Ring 
is generated by R and S.
is generated by R and S.
◊
<Definition>
R and S are integral domains that have common quotient field K.
For partial ring T=RS generated by R and S, when <Definition> simple is satisfied, it is called "Spm R ad Spm S are simple glue."
◊
<Sample>
Projective space Pn is simple glue.
◊
<Definition>
Algebraic Variety's morphism is glue of affine algebraic variety's ring homomorphism image.
Algebraic direct product is direct product of affine algebraic variety.
◊
4.
Affine algebraic variety X
Ring over k R
is called R value point of X.
Whole is called set of R value point of X, expressed by X(R).
is called set of R value point of X, expressed by X(R).
Ring homomorphism over k 
X(f) := X(R)
X(S)
X(S)
Ring homomorphism , 
, 
<Definition>
is function from ring category over k to category of set.
◊
<Definition>
Functors from ring category to set category F, G
Ring R
Family of 
over ring R {
}
over ring R {}
{} has functional morphism.
} has functional morphism.
Functors F,G have isomorphism ( or natural transformation).
Functor from ring's category to set's category that is isomorphic to algebraic variety, is called representable or represent by X, or fine moduli.
◊
<Definition>
Functor from ring's category to set's category F
When 
satisfies the next conditions, X is called coarse moduli.
satisfies the next conditions, X is called coarse moduli.
(i) There is natural transformation : 
.
: .
(ii) Natural transformation 
,
,
Morphism that satisfies 
is existent uniquely.
is existent uniquely.
(iii) For algebraic close field k' 
k, 
(k') is always bijection.
k, (k') is always bijection.
◊
<Definition>
Algebraic variety G that 
is functor to group's category is called algebraic group.
is functor to group's category is called algebraic group.
◊
<Definition>
Finite generative ring over k A
When G = Spm A satisfies 3 conditions on the next triad is called affine algebraic group.
Triad
Conditions
(i) 
are commutative for 
.
are commutative for .
(ii)There is identity map for A.
(iii) There is coincident with 
for A.
for A.
◊
5.
Projective space over C Pn
(2n+1) dimensional spherical surface 
{
}
{}
Pn has continuous surjection from 
.
.
Pn is compact.
<Definition>
Map 
is called closed map when 
is closed set image 
becomes closed set.
is called closed map when is closed set image becomes closed set.
◊
<Definition>
Algebraic variety X is called complete when projection 
is closed map for arbitrary manifold Y.
is closed map for arbitrary manifold Y.
◊
<Definition>
Morphism from complete algebraic manifold X to separated algebraic manifold Y, 
is closed map.
is closed map.
◊
<Proposition>
Projective space Pn is complete.
◊
<System>
Algebraic manifold that has closed embedding at Pn is complete.
This algebraic manifold is called projective algebraic manifold.
[Interpretation]
Here language is expressed by Pn.
Word is expressed by projective algebraic manifold.
Meaning of word is expressed by closed embedding.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
All rights reserved.
© 2011 by The Sekinan Research Field of Language
5.
Note
Provisional philosophic conjecture on additional meaning is the following.
- From symplectic geometry to Fukaya category.
- From Fukaya category to derived category.
- Kawamata conjecture at derived category.
- Smooth objective algebraic manifolds satisfies birational map.
- Fully faithful embedding exists between two manifolds.
Birational Language
Notes for KARCEVSKIJ Sergej
Stable and Unstable of Language
Symplectic Language Theory
Floer Homology Language
Notes for KARCEVSKIJ Sergej
Stable and Unstable of Language
Symplectic Language Theory
Floer Homology Language
Tokyo
23 May 2016
Read more: http://srfl-theory.webnode.com/news/additional-meaning-and-embedding/
Subscribe to:
Posts (Atom)